1. Hypothesis and Cost
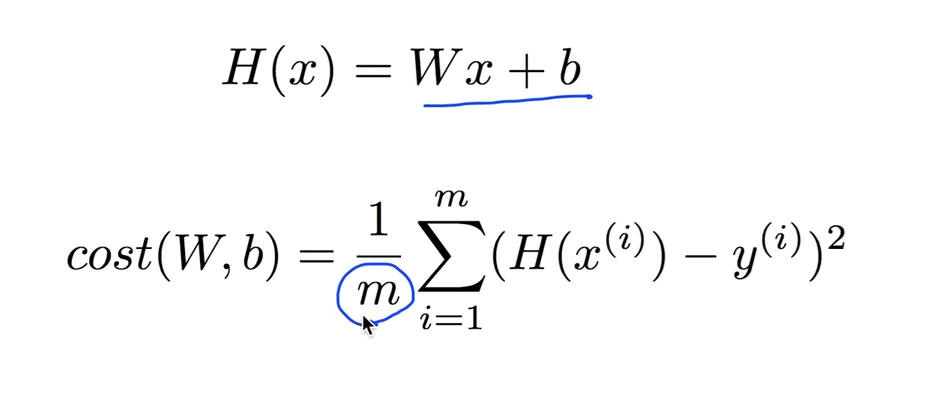
1. Hypothesis즉 우리가 구할 모델이 대략 H(x) = Wx + b로 주어질 때
2. 모델과 실제 데이터가 얼마다 같고 다른지를 나타내는 cost(W,b) function이 위와 같다.
3. 가설의 값과 실제값 차이의 제곱의 총 값을 더하고 평균을 구한다.
4. cost(W,b) function이 최소일 때의 W, b를 구한다.
2. Simplified hypothesis
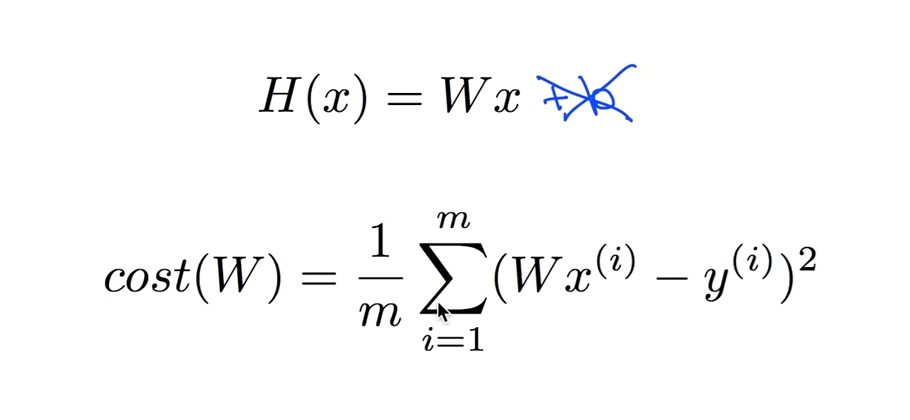
b를 없애 더 간략한 모델을 만들 수 있다.
3. What cost(W) looks like?
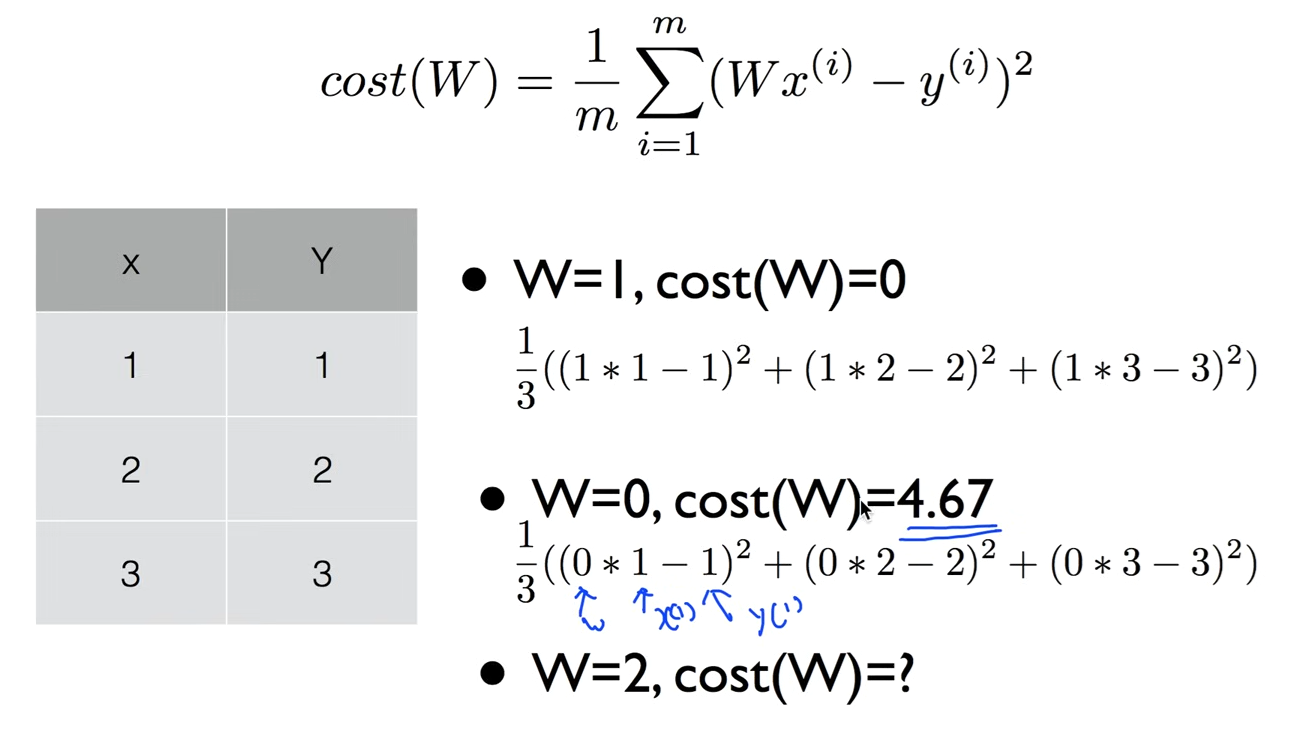
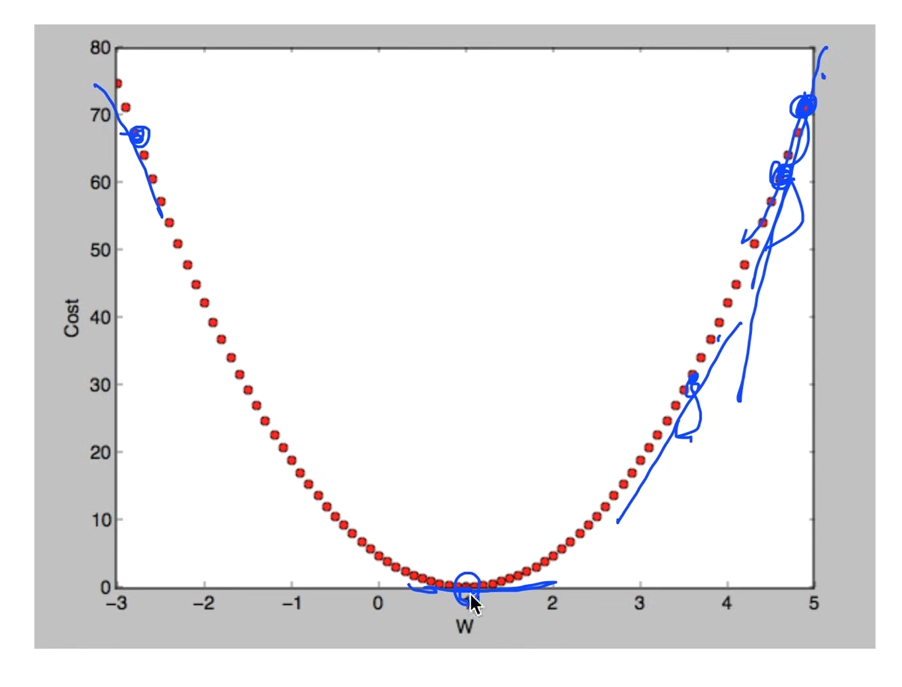
simplified 모델의 W값을 넣어서 계산해보고 이를 그래프로 나타내면
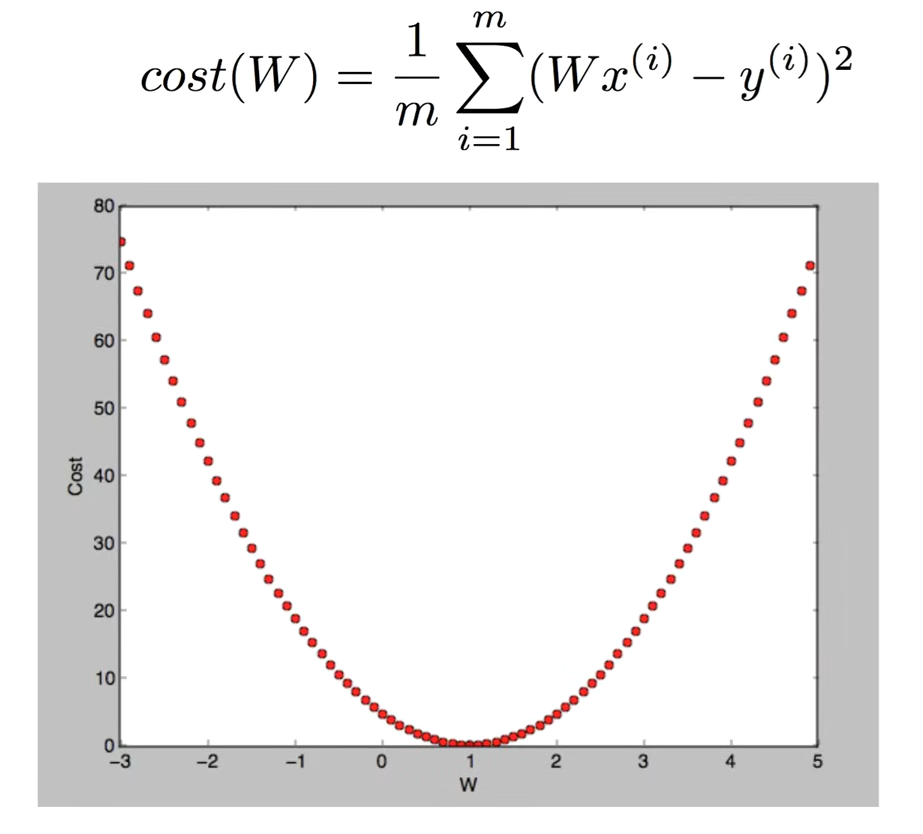
대략 위와 같이 나온다. 우리의 목표는 cost(W)가 최소가 되는 것이 목적이므로 갖고 있는 어떤 데이터를 갖고도 기계적으로 최소가 되게 하는 W를 구해야 한다.
4. Gradient descent algorithm

Gradient descent algorithm은 말 그대로 경사(Gradient)를 따라 내려가는(Descent) 방식의 알고리즘이다. 이 알고리즘은 cost function의 값을 최소화하는 W, b를 찾는 것이 목적이며, W, b 외에도 w1, w2, w3 등 다양한 파라미터가 존재하더라도 cost function을 최소화할 수 있는 최적의 값을 찾는 데 사용된다.
5. How would you find the lowest point?
미분값 구할 때, 0이 되는 지점을 구하면 된다.
6. How it works?

초기 추정값에서 시작하며, 일반적으로 (0, 0) 또는 다른 임의의 값에서 시작할 수 있다. 이후 W와 b를 조금씩 변경하면서 cost(W, b)를 줄이기 위해 시도하며, 매번 cost를 가장 많이 줄일 수 있는 방향의 기울기(gradient)를 선택한다. 이 과정을 반복하면서 cost가 최소가 되는 지점으로 수렴할 때까지 진행하게 되며, 결국 지역 최소값에 도달하게 된다. 이 알고리즘은 어디서 시작하느냐에 따라 도달하는 최소값이 달라질 수 있다는 흥미로운 특성을 가지고 있다.
7. Formal definition
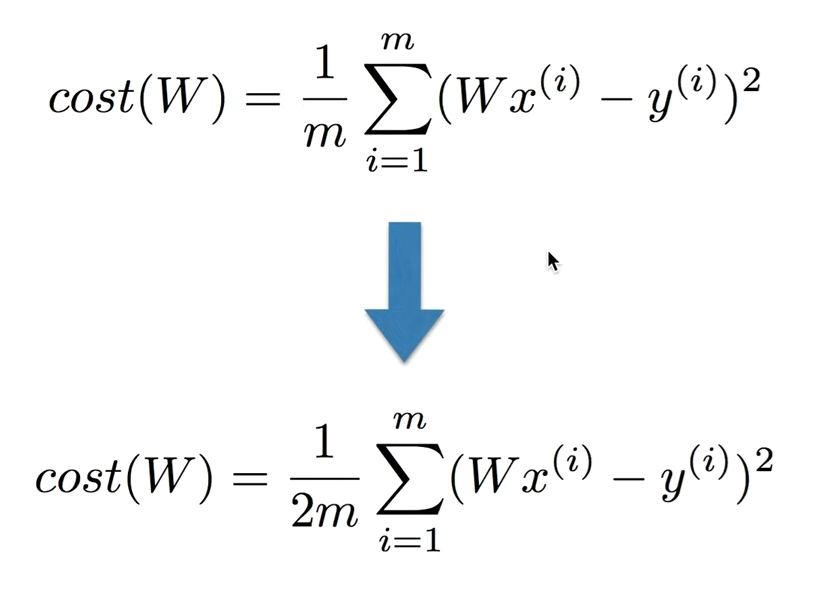
미분을 쉽게하기 위해 m을 2m으로 바꾼다.
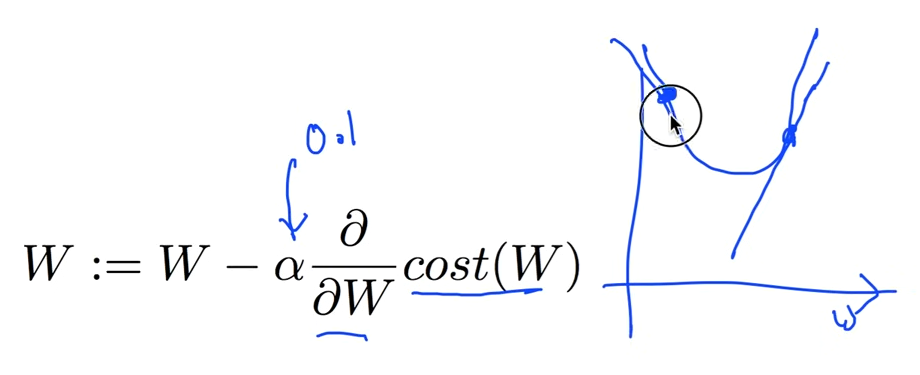
α는 상수이며,
1. 오른쪽에서 접근할 경우, ∂W는 W의 변화량으로 음수가 되기 때문에 앞에 마이너스(-)가 붙는다.
2. 왼쪽에서 접근할 경우에도 기울기가 음수이므로 마찬가지로 앞에 마이너스가 붙는다.
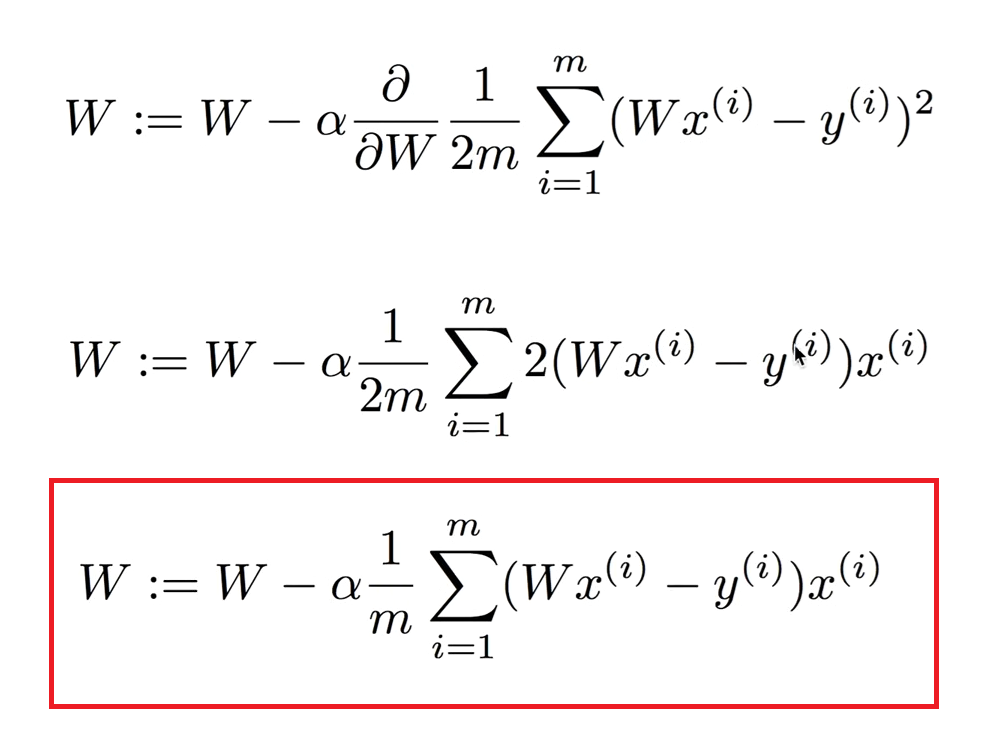
따라서 미분을 통해 아래와 같은 식을 얻게된다. 이 수식이 Gradient descent algorithm이다.
8. Convex function
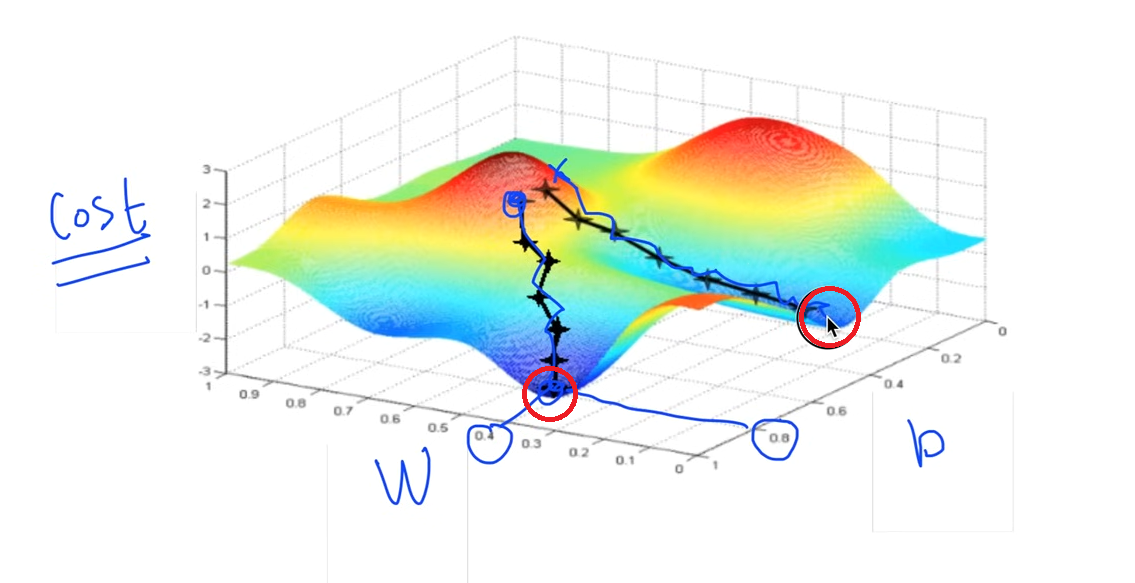
w, b에 대한 cost functino이 위와 같을 때 어떤 지점을 타고 내려오느냐에 따라 W, b가 달라진다.
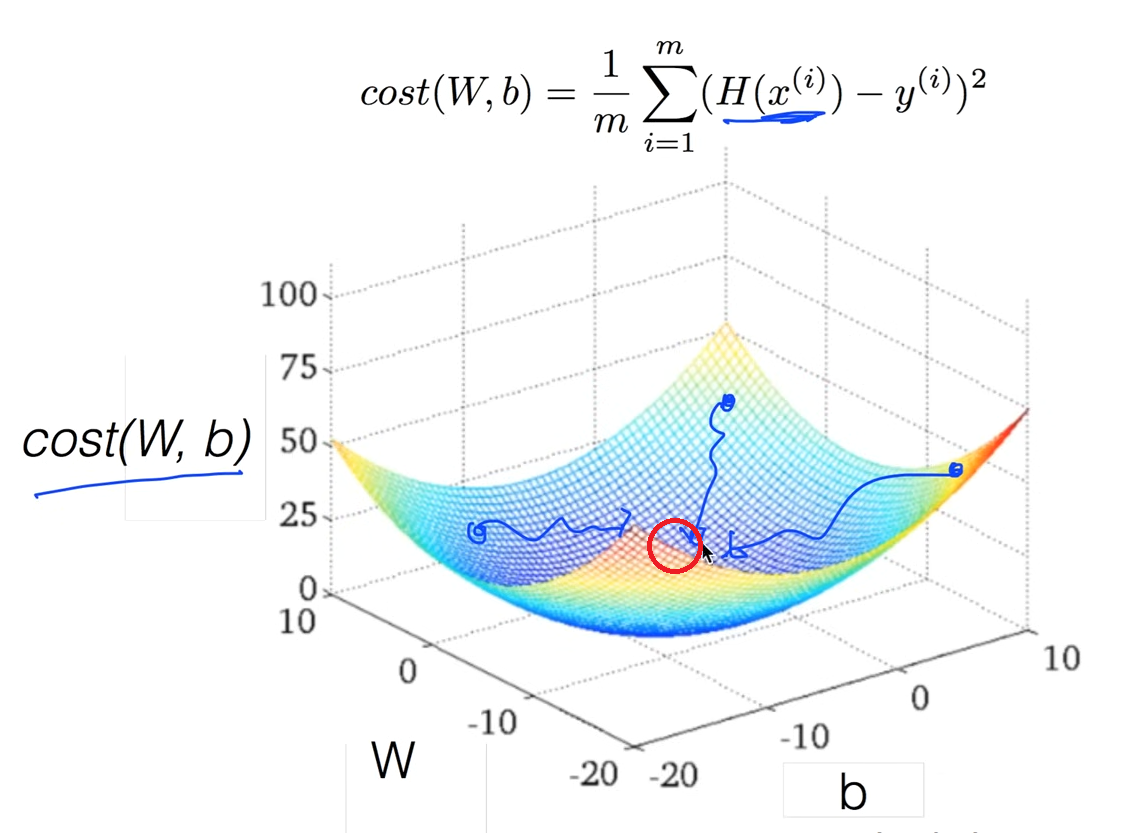
위와 같은 형태의 그래프를 Convex function이라고 한다. 어느 지점에서 시작하든 W, b가 같다. 따라서 Gradient descent algorithm을 사용하기 위해서는 cost 모델을 설계할 때 그래프의 모양이 Convex function 인지 확인해야한다.
'Python > ML' 카테고리의 다른 글
| [ML] 2025/07/22, multi-variable linear regression (0) | 2025.07.22 |
|---|---|
| [ML] 2025/07/22, Linear Regression의 cost 최소화의 TensorFlow 구현 (0) | 2025.07.22 |
| [ML] 2025/07/21, TensorFlow로 간단한 linear regression을 구현 (0) | 2025.07.21 |
| [ML] 2025/07/21, Linear Regression의 Hypothesis 와 cost 설명 (0) | 2025.07.21 |
| [ML] 2025/07/21, TensorFlow의 설치및 기본적인 operations (0) | 2025.07.21 |