1. Regression

- Hypothesis는 입력 X에 대한 선형 함수이며, 우리가 찾고자 하는 가설 함수이다.
- Cost(W)는 설정한 Hypothesis와 실제 학습 데이터 간의 오차를 측정한 값으로, 두 값의 차이를 제곱한 후 평균을 구해 계산한다.이 Cost를 최소화하는 W를 찾는 것이 목표이다.
- Cost 함수의 그래프는 U자 형태로, 어느 지점에서 시작하더라도 경사를 따라가면 결국 최소값에 도달하게 된다. Gradient Descent 알고리즘에서는 α(알파)를 step size라고 하며, 이를 learning rate라고도 부른다. α는 기울기를 따라 얼마나 이동할지를 결정하는 값이다.
2. (Binary) Classification

Classification은 스팸 필터링뿐 아니라, Facebook이 타임라인을 사용자에게 맞게 추천할 때에도 활용되는 문제 유형이다.
3. 0, 1 encoding

스팸인지 아닌지로 나타내지 않고 1, 0 두 숫자를 통해 나타낸다.
4. Pass(1)/Fail based on study hours
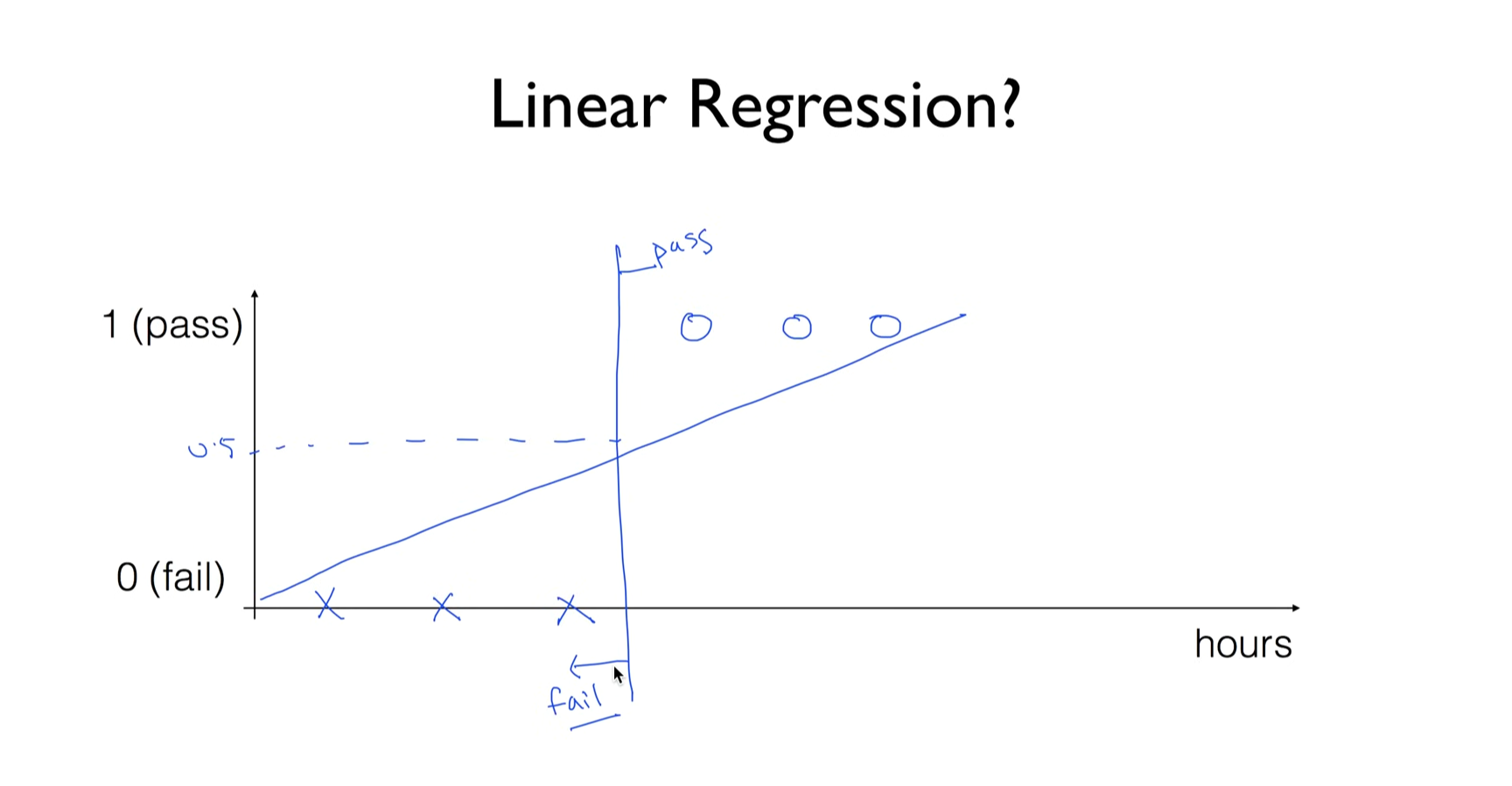
시험에 합격하고 떨어지는 것을 갖고 예를 들어보자. classification이 아니라 linear regression으로 hypothesis를 세워서 예측할 수 있지 않을까 생각이 들지만

시간을 50시간 투자한 데이터를 기준으로 pass가 1인 값을 사용해 Linear Regression을 적용하면, cost 값을 줄이기 위해 기울기가 점차 감소하게 된다.
이때 0.5를 기준으로 합격과 불합격을 구분하는 선을 설정했지만, 학습 과정에서 이 기준선이 이동하면서 실제로는 합격인 데이터도 0.5보다 작게 예측되어 불합격으로 잘못 분류되는 현상이 발생한다.
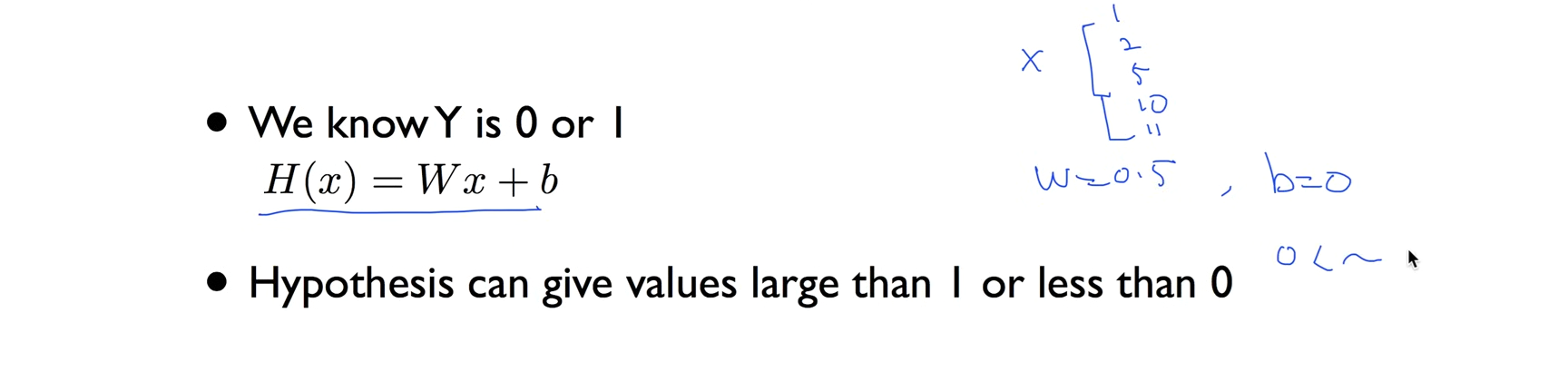
Classification 문제에 Linear Regression을 적용하면 출력 값이 0과 1 사이로 제한되지 않기 때문에 문제가 발생한다.
예를 들어, 학습을 통해 W = 0.5, b = 0인 Hypothesis를 얻었다고 가정하면, 입력 x에 100이 들어갈 경우 출력은 50이 된다. 이처럼 예측 값이 1보다 크거나 0보다 작을 수 있어 확률처럼 해석하기 어렵고, 이로 인해 분류 기준을 명확하게 설정할 수 없게 된다.
5. Sigmoid

Linear한 함수 대신 우리가 구하고자 하는 함수 g(z)는, z 값에 상관없이 항상 0에서 1 사이의 값을 가지는 함수여야 한다.
이러한 조건을 만족하는 함수가 바로 Sigmoid 함수이다.또 logistic function이라고 부른다.
6. Logistic Hypothesis



'Python > ML' 카테고리의 다른 글
| [ML] 2025/07/22, multi-variable linear regression을 TensorFlow에서 구현하기 (0) | 2025.07.22 |
|---|---|
| [ML] 2025/07/22, multi-variable linear regression (0) | 2025.07.22 |
| [ML] 2025/07/22, Linear Regression의 cost 최소화의 TensorFlow 구현 (0) | 2025.07.22 |
| [ML] 2025/07/22, Linear Regression의 cost 최소화 알고리즘의 원리 설명 (0) | 2025.07.22 |
| [ML] 2025/07/21, TensorFlow로 간단한 linear regression을 구현 (0) | 2025.07.21 |